글 | 강성훈
KTX가 출현하기 전에 고급 열차는 새마을호이었고, 시속 100km로 주행하였다. 그 후 KTX가 출현하여 300km/h로 주행하였다. 그런데 KTX를 처음 타본 사람들의 반응은 생각보다 빠르지 않다고 했다. 100km/h로 주행한 것이 300km/h로 주행하면 3배로 빨라질 것이라고 생각했는데 조금 더 빨라진 느낌이 든 것이다. 100km/h보다 2배로 빨라진 것으로 느끼기 위해서는 200km/h가 아니고 1000km/h로 주행해야 한다. 즉, 물리적으로 10배 속도로 주행해야 인간은 2배로 빨라졌다고 느끼는 것이다. 이것이 인간의 감각의 법칙이고, 이러한 현상을 설명하기 위해서 데시벨이 도입되었다.
한 네티즌은 SNS에 “가격은 일반 라면의 3배인데, 맛은 3배 더 맛있지 않다”고 썼다.
다른 네티즌은 “눈이 튀어나올 정도로 차별화된 맛은 아닌 것 같다”며“이 돈 주고
사먹기엔 비싸다는 생각이 든다”고 밝혔다.
최근에 다음과 같은 글이 SNS에 올라온 적이 있다. 라면 값이 3배이면 맛이 3배로 맛있어지는 것으로 착각하고 있는 것이다. 이와 같이 인감의 감각은 물리적인 양과 비례 관계가 성립되지 않는다. 음향 기기의 사양서에 dB(decibel, 데시벨)이라는 단어가 수도 없이 많이 나온다. 앰프의 증폭도는 50dB, 또 주파수대역은 -3dB로 나타내거나 스피커의 감도는 90dB, S/N 비 86dB, 왜곡률 -40dB와 같은 용어를 음향 기기의 사양이나 카탈로그에서 흔히 볼 수 있다. 데시벨은 음향 분야에서만 사용하는 것이 아니고, 전력, 전압, 전류, 전파 등 여러 분야에서 사용하는 단위이다.
XdB가 아니고 몇 배라고 표현하면 누구나 알기 쉬울 것 같은데, 왜 dB를 사용하는가? 이것은 인간의 감각은 물리적 자극이 2, 4, 8배와 같이 증가되어야 감각적으로 같은 변화로 느끼기 때문이다. 예를 들어 앰프의 출력을 10W에서 20W로 2배 증가시켰을 때 느끼는 음량의 변화와 100W를 200W로 2배 증가시켰을 때 음량 변화에 대한 느낌이 같은 것이다.
또, 레벨 10의 음량이 스피커로부터 나온다고 하자. 그리고 스피커 레벨을 5로 하면 음량은 절반이 되고, 반대로 레벨을 20으로 하면 음량은 2배가 된다. 이때 5와 10의 레벨 차이는 5이고, 비로 표현하면 2배가 된다. 또, 10과 20의 차이는 10이고 비는 2배가 된다. 따라서 10과 5의 차이와 10과 20의 차이는 다르지만, 이 차이의 비는 2이고, 대수(로그, logarithm)로 나타내면 둘 다 3dB(=10log2)이다. 이 두 경우는 대수 값이 같으므로 같은 변화의 크기로 느낀다.
이와 같이 청각은 음량 변화를 절대량으로 느끼는 것이 아니고, 변화의 비율에 비례(대수 비례)하여 느끼는 것이다. 음향 기술에서 데시벨(dB)를 사용하는 이유는 이러한 인간의 청각 특성 때문이다. 즉, 인간의 감각적 지각 변화와 비슷한 에너지 변화를 표현하는 단위가 데시벨이다. 따라서 앰프의 볼륨과 믹서 페이더도 인간의 변화 감각과 일치하도록 로그 볼륨을 사용하고 있다.
또, 음의 세기는 아주 넓은 범위를 취급하므로 숫자가 너무 커서 사용하기 불편하다. 사람이 들을 수 있는 가장 큰 음압과 가장 작은 음압의 차이는 100만 배의 차이이지만, 로그로 나타내면(20log 106=120dB) 3자리 수자로 나타낼 수 있다. 이와 같이 큰 수를 데시벨로 표기하면 작게 표현할 수 있으므로 편리하다. 그리고 로그 연산은 다른 많은 편리한 점들이 있다.
1. 로그의 정의
10의 2승(=10(2))은 100이다, 반대로 10을 몇 승하면 100이 되는가? 답은 2이다. 그리고 10의 3승(=10(3))은 1000이다. 이 관계를 설명하기 위하여 log라는 기호를 도입하여 다음과 같이 표기하고, 이것을 상용 로그(common logarithm)라고 한다.
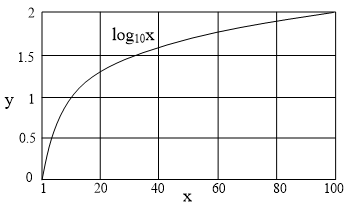
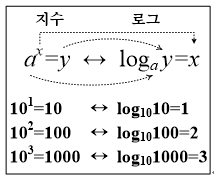
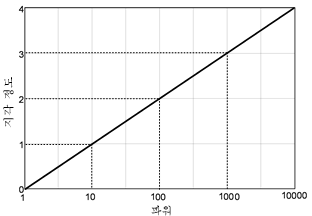
이와 같이 로그로 나타내면 1000이나 10000과 같은 3자리나 4자리 수치를 한자리 수치로 나타낼 수 있다. 그림 1은 선형 함수 그래프이고, 그림 2는 로그 함수 그래프이다. 그림 3은 지수와 로그 함수와의 관계를 나타내고 서로 역 함수이다.
log 10(1) =0
log 10(10) =1
log 10(100) =2
log 10(1000) =3
2. Bel(벨)의 정의
Bel은 (1) 식과 같이 두 파워의 비에 log를 취한 것이다.
Bel=log(P2/P1) [B] (1)
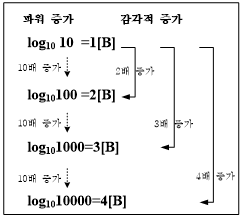
따라서 (P2/P1)가 10이면 1 Bel, 100이면 2 Bel이 된다. 이것은 그림 4~5와 같이 파워가 10배씩 증가되면, 감각적으로는 배씩 증가되는 것이다. 표 1과 같이 파워가 10배 증가되면 음량의 크기도 2배로 커진 느낌이 든다.
| 파워 증가 | 음량 변화 지각의 정도 | 음압 레벨 변화 |
| 100배 | 4배로 커진 느낌 | 20dB |
| 10배 | 2배로 커진 느낌 | 10dB |
| 1 | 기준 | 0dB |
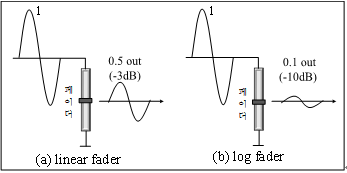
이러한 청각 특성 때문에 음향 기기에서 로그 볼륨을 사용한다. 예를 들어 그림 6(a)와 같이 선형 페이더를 중간에 놓으면 파워는 1/2(=-3dB)로 감소되고, 페이더를 절반으로 줄였는데도 음량이 작아진 느낌이 들지 않는다. 즉, 페이더의 위치와 음량의 감각적인 변화 정도가 일치하지 않는다. 그러나 그림 6(b)와 같이 로그페이더를 중간에 놓으면 파워가 1/10(= -10dB)로 감소되고, 음량이 절반으로 작아진 느낌이 들므로 페이더의 위치와 음량의 감각적인 변화 정도가 일치한다.
3. deciBel(데시벨)의 정의
Bel은 단위가 작아서 사용하기 불편하여 deciBel(dB)을 사용한다. deciBel은 Bel에 1/10 배를 의미하는 deci(d)를 붙인 것이고, Bel은 전화 발명자 이름을 따른 것이다. 기준 파워를 P1, 비교하고자 하는 파워는 P2라고 하면, 데시벨은 다음과 같이 정의된다.
deciBel=10log(P2/P1) [dB] (2)
데시벨은 기본적으로 파워의 비이지만, 전압이나 전류의 비도 사용할 수 있다. 파워는 전압이나 전류의 제곱에 비례하므로 전압의 데시벨은 그림 7과 같이 20log을 곱한다.
파워 데시벨 → 10log(P2/P1) [dB]
전압 데시벨 → 20log(V2/V1) [dB]
전류 데시벨 → 20log(I2/I1) [dB]
그림 7. 데시벨의 공식
4. 데시벨의 합 계산
40+40=80이지만, 40dB+40dB=80dB가 아니다. 80은 40의 2배이지만, 80dB는 40dB의 2배가 아니다. 40dB는 10log10X이므로 X(=10000) 값을 구하여 더하고, 이 두 값을 더한 것(=20000)에 다시 log로 바꾸어야 한다(=10log20000).

40dB+40dB=?
40dB = 10log10X → log10X=4 → X=104
40dB+40dB → 10 +10 를 로그로 바꾸면
10log(10(4) +10(4) )=10log20000=43dB 또는
40dB+40dB → 10log(10(40)/(10)+10(40)/(10))=43dB
5. 로그의 연산
(1) logXY = logX+logY
예) log(100)=log(10×10) = log10+log10=1+1=2
(2) log(X/Y) = logX-logY
예) log(10) =log(100/10)= log100-log10=2-1=1
(3) logXn = nlogX
예) log100 =log102=2 log10=2
데시벨을 사용하면 다음과 같은 점들이 편리하다. |
① 숫자가 수 천 또는 수만 배 이어도 dB로
표현하면 두 세자리 수로 나타낼 수 있다.
② 증폭도나 감쇠도를 계산할 때 각각의 합 또는 차로 사용한다. 증폭도(이득)와 감쇠도(손실)를 +와 -의 기호로 표시하여 쉽게 계산할 수 있다.
예를 들면, 증폭도는 곱하고 감쇠도는 나누지만, dB로 계산하면 더하기와 빼기로 계산하므로 간편하다. 산술 계산 a × b ÷ c = x
dB 계산 A + B – C = X[dB]
③ 그림 9와 같이 주파수 특성을 로그 그래프로 표현하면 작은 값에서 큰 값까지 한번에 비교하여 작은 용지에 표현할 수 있으므로 편리하다.
그림 9의 주파수 특성 그래프에서 10Hz → 100Hz, 100Hz → 1000Hz, 1000Hz → 10000Hz의 변화는 전부 같은 크기의 변화로 느끼는 것이다. 즉, 변화량은 10배이고, 전부 같은 변화량으로 느끼는 것이다. 따라서 주파수 특성 그래프는 그래프를 사용하지 않고 로그 그래프를 사용하는 것이다.
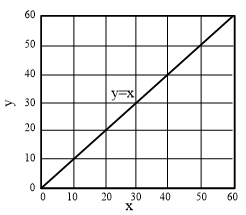
피아노 건반은 그림 10과 같이 로그 스케일로 구성되어 있다.
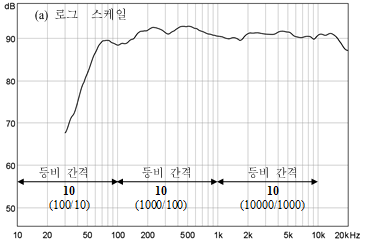
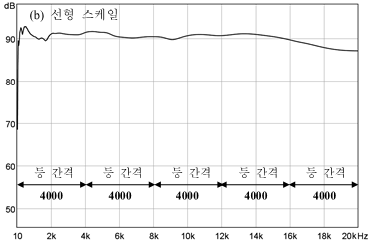
그림 9. 스피커 특성을 로그 스케일과 선형 스케일로 나타낸 예