글|강성훈
40dB+40dB는 얼마인가? [표 1]과 같이 두 신호의 위상 차에 따라서 데시벨의 합이 달라진다.
| 40dB+40dB=46dB | 두 신호가 동위상인 경우의 합, 6dB 증가 | ||
| 40dB+40dB=43dB | 두 신호의 위상 차가 90도인 경우의 합, 3dB 증가 | ||
| 40dB+40dB=40dB | 두 신호의 위상 차가 120도인 경우의 합, 0dB 증가 | ||
| 40dB+40dB=0dB | 두 신호가 역위상인 경우의 합, 상쇄됨 |
콘서트홀의 음향 시스템을 설계할 때, 음압 레벨을 크게 하고 커버리지를 넓게 하기 위해서 여러 대의 스피커를 조합하여 사용하는 경우가 많다. 또, 오케스트라에서 같은 악기를 많은 연주자들이 연주한다. 이것은 한 대의 악기로는 음량이 작으므로 여러 대의 악기로 연주하여 음량을 크게 하고, 코러스 효과로 풍부한 음색을 얻기 위한 것이다. 여러 대의 스피커를 사용하는 경우나 여러 대의 악기를 연주하는 경우에 음압 레벨이 얼마나 증가되는가? 본 고에서는 여러 개 음원의 레벨(dB)을 더하는 방법에 대해서 설명한다.
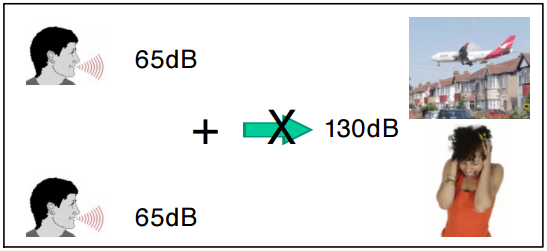
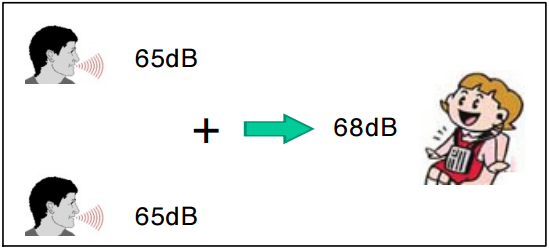
대면 대화 시 음성의 레벨은 65dB 정도이다. 만약 두 사람이 발성하면 [그림 1]과 같이 130dB(=65dB+65dB)가 되는가? 130dB는 청각에 통증이 오고 고막이 파손되는 엄청나게 큰 음압 레벨이다. 이것은 무엇인가 문제가 있다. 두 사람이 발성하면, [그림 2]와 같이 음압 레벨은 3dB가 증가되어 68dB가 되고 듣기 편안한 레벨이다. 65+65=130이지만, 65dB+65dB=130dB가 아니다. 데시벨의 합은 그냥 더하면 안 된다.
1. 데시벨의 합 계산

40+40=80이지만, 40dB+40dB=80dB가 아니다. 80은 40의 2배이지만, 80dB는 40dB의 2배가 아니다. 40dB는 10log10X이므로 X(=10000)값을 구하여 더하고, 이 두 값을 더한 것(=20000)에 다시 log를 취해서 계산해야 한다(=10log20000).
40dB+40dB=?
40dB = 10log10X ⇒ log10X=4 ⇒ X=104
40dB+40dB ⇒ 10 +10 를 데시벨로 계산하면, 10log(10 +10 )=10log20000=43dB 또는 40dB+40dB ⇒ 10log(1040/10+1040/10)=43dB
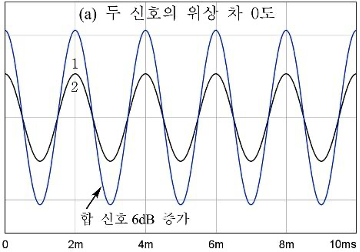
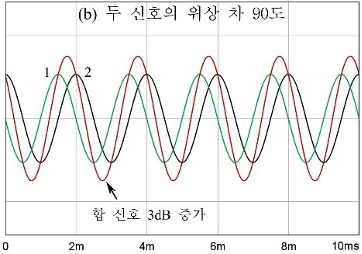
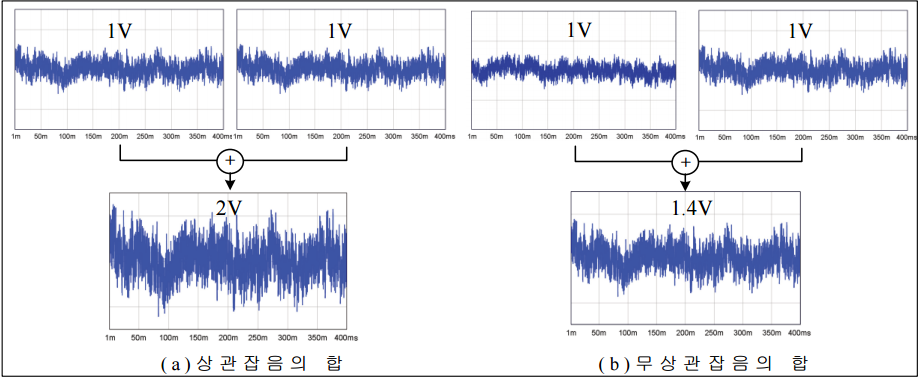
1+1은 두 신호의 위상 차에 따라서 두 신호의 합의 크기가 달라진다. [그림 4]에는 위상 차에 따른 두 신호의 합을 벡터도로 나타낸다. 두 신호의 위상 차가 0도이면 합은 2(20log2=6dB)가 되고, 위상 차가 90도이면 합은 1.4(10log2=3dB), 위상 차가 120도이면 합은 1(20log1=0dB), 위상 차가 180도이면(방향이 반대) 합은 0이 된다.

2. 음원들의 상관에 따른 음압 레벨 합
두 음원은 두 대의 스피커일 수도 있고, 두 사람이 바이올린을 연주하거나 두 대의 기계 소음일 수도 있다. 두 대의 스피커에서 재생되는 음의 파형들은 완전히 똑같다. 반면에 두 사람이 같은 악기를 연주할 때나 두 대의 기계에서 소음이 발생되는 경우에 이 두 음원의 파형은 완전히 다르다.
두 신호의 파형이 완전히 같으면 두 신호의 상관도는 1이 되고, 위상 차는 0도가 된다. 이것을 상관 음원(Correlated Signals)이라고 한다. 또, 두 신호의 파형이 완전히 다르면 두 신호의 상관도는 0이 되고, 위상 차는 90도가 된다. 이것을 무상관 음원(Uncorrelated Signals)이라고 한다.
[그림 5(a)]와 같이 두 신호가 완전 상관인 경우에는 두 신호의 위상 차는 0도이고, 두 신호의 합은 2(20log2=6dB)가 된다. 또, 두 신호가 무상관인 경우에는 [그림 5(b)]와 같이 두 신호의 위상 차는 90도이고, 두 신호의 합은 1.4(20log1.4=3dB)가 된다. [그림 6(a)]는 동위상 잡음 신호(상관 신호)의 합을 나타내고, [그림 6(b)]는 90도 위상 차가 있는 잡음 신호(무상관 신호)의 합을 나타낸다.두 신호의 위상 차가 120도이면 부분 상관이고, 두 신호의 합은 1(20log1=0dB)이 된다. 두 신호의 위상 차가 180도이면 두 신호의 합은 0이 된다. 이와 같이 두 신호의 레벨 합을 구하는 방법은 두 신호들의 상관 정도에 따라서 달라진다.
1) 무상관 음원들의 레벨 합
무상관 음원들의 음압 레벨이 L1, L2 … Ln[dB]인 경우에 전체 음원의 음압 레벨의 합(LT)은 (1)식으로 구하고, n개 음원들의 레벨(L)이 전부 같으면 (2)식으로 구한다.
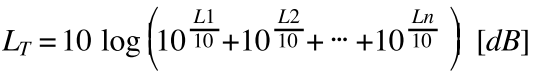
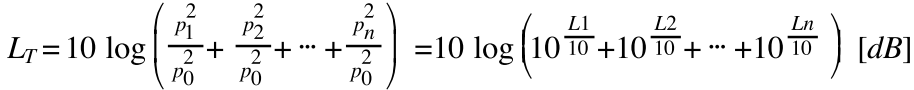
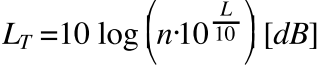
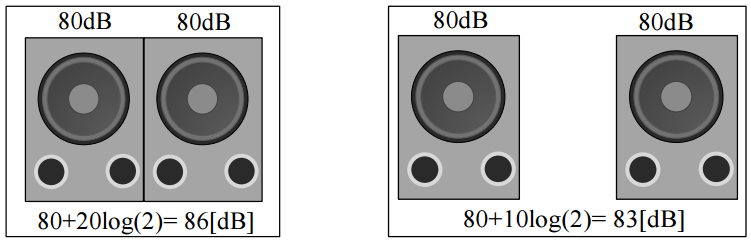
예를 들어 1대의 바이올린 음압 레벨이 80dB이면, 2대의 음압 레벨은 160dB가 아니고 (3)식과 같이 83dB 가 된다.
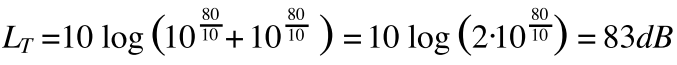
이와 같이 악기의 대수가 2배로 증가되면, [그림 7]과 같이 음압 레벨의 합은 3dB 증가된다. 이것은 음원 간의 상관이 전혀 없는 악기 음 이외에 소음원도 마찬가지로 음원이 두 배씩 증가되면 음압 레벨은 3dB씩 증가된다.

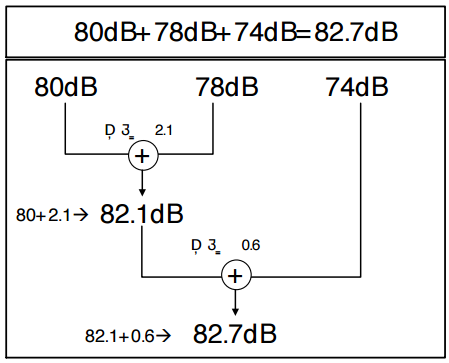
음압 레벨의 합 계산을 간단히 하는 방법은 [표 2]를 사용하는 것이다. 예를 들면, 표에서 L1 – L2 의 보정치 a[dB]를 구하고, 이 값을 큰 값인 L1에 더해주면 된다. 3개 이상의 합은 [그림 8]과 같이 큰 값부터 차례로 두 개씩 더해 가면 된다.

그리고 두 음원의 합성 레벨을 구할 때, 두 음원의 레벨 차가 10dB이면 레벨이 큰 음원에 0.4dB 더하면 합의 레벨이 되고, 레벨 차가 20dB이면 두 음원의 합 레벨은 큰 음원의 음압 레벨과 같다. 소음이 있는 환경에서 측정하고자 하는 신호의 음압 레벨이 소음 레벨보다 20dB 이상이어야 하는 것은 이러한 이유 때문이다.
2) 상관 음원들의 레벨 합
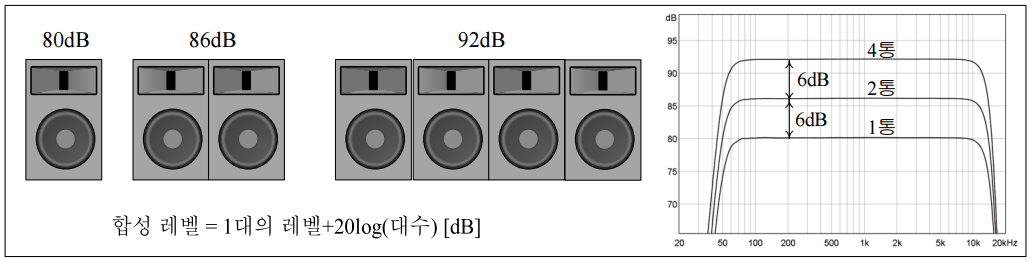
[그림 8]과 같이 스피커가 여러 대 붙어있고, 스피커에 주파수와 위상이 같은 음원(상관 음원)을 입력하여 재생하면 합성 음압 레벨은 (4)식으로 계산하고, 스피커 레벨(L)이 전부 같으면 (5)식으로 계산한다.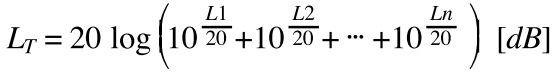
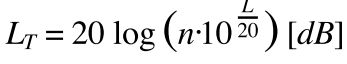
음원들이 완전 상관인 경우에는 음원이 2배가 되면, [그림 9]와 같이 음압 레벨이 6dB 증가된다. 그러나 스피커 간의 간섭 때문에 이론대로 음압 레벨이 증가되지 않는 경우가 있다. 그리고 두 스피커에 무상관 음원을 따로 따로 입력하면 3dB 증가된다. 또, 홀에서 무대 좌우에 2대의 스피커가 설치된 경우에는 무상관 음원이 되므로 음압 레벨이 3dB 증가된다. 마찬가지로 [그림 10]과 같이 2대의 서브우퍼가 붙어 있는 경우에는 상관 음원이므로 6dB 증가되지만, 떨어져 있으면 두 스피커의 음이 무상관이 되어 3dB 증가된다.
참조 동영상; 음향기술총론 데시벨의 합 계산













