임피던스란 II

글 | 강성훈

 믹서, 앰프, 마이크 등 음향 기기들의 스펙을 보면 임피던스(impedance)라는 용어가 나온다. 입력 임피던스(input impedance), 출력 임피던스(output impedance), 종단 임피던스(terminating impedance), 정합 임피던스(matched impedance) 등등 많은 용어들이 있다. 임피던스는 믹서, 앰프, 스피커의 특성을 이해하는데 아주 중요하다. 음향 수학 코너에서는 임피던스와 관련된 내용을 다음과 같은 순서대로 설명해 간다.

1.  임피던스란, 복소수
2.  저항과 임피던스, 유도성 회로
3.  용량성 회로, 유도성 용량성 회로
4.  스피커의 임피던스, 앰프의 출력 임피던스, 스피커 레벨과 라인 레벨 임피던스
5.  기기의 입출력 임피던스 구하기
6.  임피던스 매칭
7.  임피던스 브리징

2. 저항과 임피던스

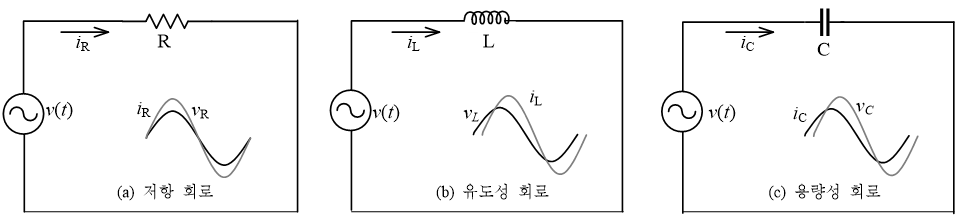
 저항만 있는 회로에서는 그림 1(a)와 같이 전압과 전류가 동위상이므로 전압과 전류 비가 저항 값(R)이 된다. 그러나 그림 1(b), (c)와 같이 인덕터(L)와 커패시터(C)가 포함되어 있는 회로에서는 전압과 전류가 위상이 다르므로 위상 차에 따라서 저항 값이 변하고 이것을 임피던스(impedance; Z)라고 한다. Impede는 ‘방해하다’는 의미이다. 직류 회로에서는 저항이 전류의 흐름을 방해하고, 교류에서는 임피던스가 전류의 흐름을 방해하는 것이다.

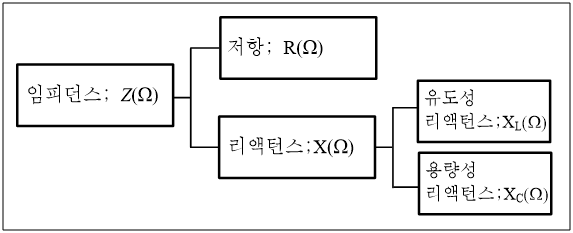
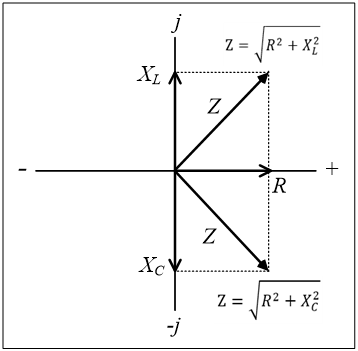
임피던스는 저항과 리액턴스로 구성되어 있다(그림 2). 리액턴스는 유도성 리액턴스와 용량성 리액턴스가 있다. 임피던스에서 실수 축에 해당하는 것이 저항이고, 허수 축에 해당하는 것이 리액턴스(X)이다(그림 3). 따라서 임피던스를 이해하기 위해서는 복소수를 이해해야 한다.

3. 유도성 회로

1) 인덕터의 특성

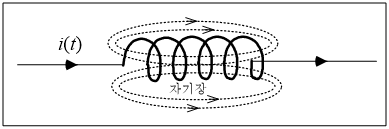
 그림 4와 같이 도선을 감아서 코일을 만들면 인덕터(inductor)가 된다. 인덕터에 전류가 흐르면 자기장이 형성되고, 전류가 변하면 자기장도 변화된다. 전류가 증가하면 자기장이 확장되고, 전류가 감소하면 자기장은 축소된다. 또한 자기장이 변하면 전류의 변화를 방해하는 방향으로 인덕터 양단에 유도 전압(induced voltage)이 발생된다. 인덕터가 가지고 있는 고유의 성질을 인덕턴스(inductance)라고 하며, 기호는 L로 나타내고, 단위는 H(Henry)이다.

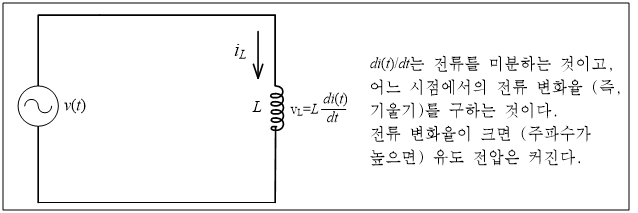
 인덕턴스는 전류의 변화에 따라 유도 전압을 만들어 내는 인덕터의 능력을 말한다. 전류가 변하면 자기장이 변하여 인덕터 양단 간에 전류의 변화를 방해하는 방향으로 유도 전압이 발생되고, 유도성 회로라고 한다. 인덕터의 유도 전압(v_L)은 그림 5와 같이 인덕턴스(L)와 전류의 시간 변화율(di/dt)에 따라서 달라지고, (1) 식과 같다. 그러므로 인덕터의 전류 변화가 빠를수록(주파수가 높을수록) 유도 전압이 커지고, 인덕턴스가 클수록 유도 전압이 커진다.

v_L = L (di(t))/dt          (1)

인덕턴스의 단위는 헨리(Henry; H)이다. 코일에 흐르는 전류가 1초당 1암페어의 비율로 변화하고, 1볼트의 전압이 유도될 때의 인덕턴스를 1H로 정의한다. 인덕턴스는 저항과 같이 전류의 흐름을 방해하는 것이다. 전선을 100회 감은 코일보다 1000회 감은 코일이 전압 변화에 대한 전류의 변화가 느리므로 같은 전류를 흘리는데 높은 전압이 필요하고, 인덕턴스가 큰 것이다. 1H는 아주 큰 단위이고, 실제로는 mH 또는 µH를 주로 사용한다.

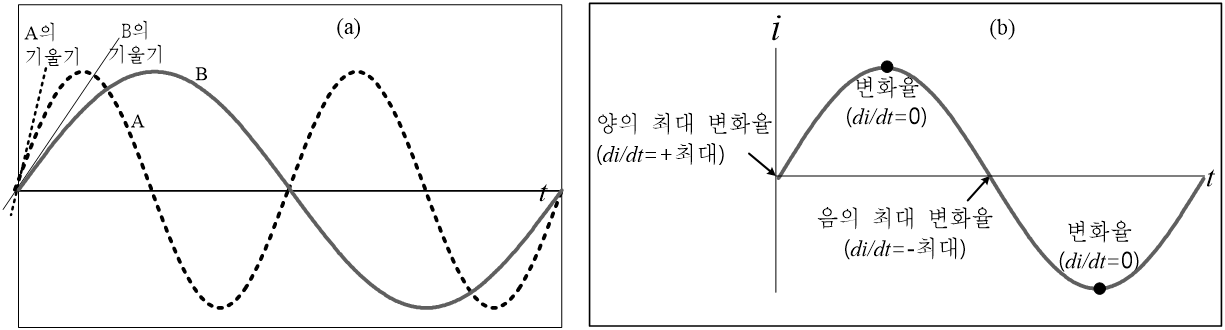
(1) 식으로부터 알 수 있듯이 유도 전압은 인덕터에서의 전류 변화가 빠를수록(즉, 주파수가 높을수록) 그림 6(a)와 같이 전류 변화가 급격하고 유도 전압이 커진다. 그림 6(b)와 같이 di/dt가 + 방향으로 최대가 되면 유도 전압은 + 최대가 되고, di/dt가 – 방향으로 최대가 되면 유도 전압은 – 최대가 된다. 그리고 전류의 변화율이 0이면 유도 전압은 0이 된다.

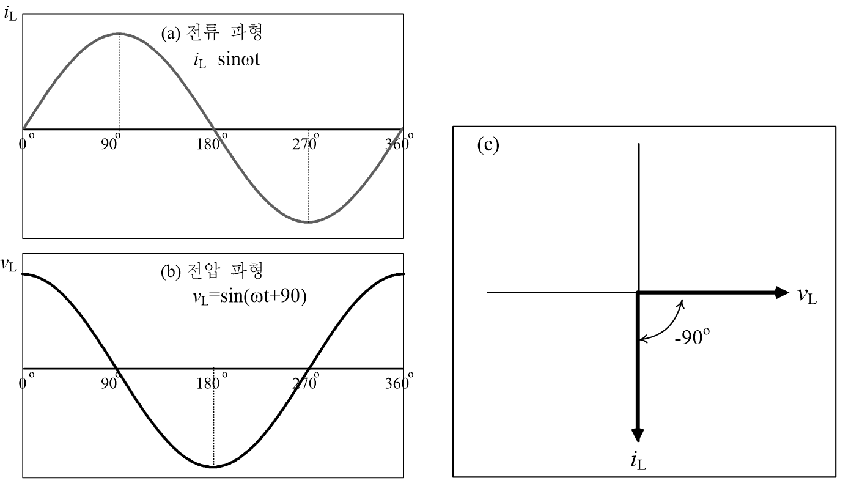
그림 7(a) (b)는 유도성 회로에서 전류와 전압 파형을 나타내고, 전류가 전압보다 위상이 90도 늦는 것을 알 수 있다. 그림 7(c)는 전압과 전류의 위상 관계를 페이저로 나타낸 것이다. 전류와 전압의 위상 차가 90도인 것은 순수 유도성 회로의 경우이고, 저항이 같이 포함된 경우에는 소자의 값에 따라서 위상 차가 달라진다(예제 2 참조).

2) 유도성 리액턴스

유도성 리액턴스(inductive reactance)는 전류에 대한 저항 값이며, 단위는 옴(Ohm)이고, 기호는 X_L로 표기한다. X_L은 v_L=L(di/dt)로부터 전류의 변화율은 주파수와 관계가 있고, 전류 변화가 빠르다는 것은 주파수가 높은 것을 의미한다. 주파수가 높으면 영 교차점에서 경사가 급격하다. 즉, 영 교차점에서 di/dt가 크다. 따라서 주파수가 증가하면 di/dt가 증가하고 v_L이 증가한다. 주파수가 낮아지면 di/dt가 감소되고, v_L도 감소된다. 유도 전압이 증가한다는 것은 저항(X_L)이 크다는 것을 의미한다. 따라서 X_L은 유도 전압의 주파수에 비례한다. 그리고 di/dt가 일정하고 인덕턴스가 변하는 경우에 L이 증가하면 유도 전압이 증가되고, L이 감소되면 유도 전압이 감소된다.

X_L은 주파수와 인덕턴스에 비례하므로 (2) 식으로 나타낸다. 2π는 비례 상수이고, 사인파의 회전 운동과 관계된다.

X_L = 2πfL[Ω]            (2)

그림 8과 같이 인덕터에 DC를 가하면 X_L은 0Ω(short 상태)이 되고, 주파수가 아주 높은 신호를 가하면 X_L은 ∞Ω(open 상태)이 된다. 

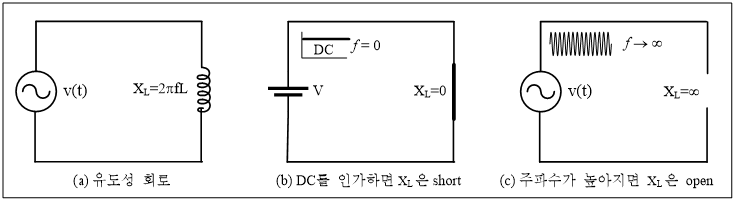
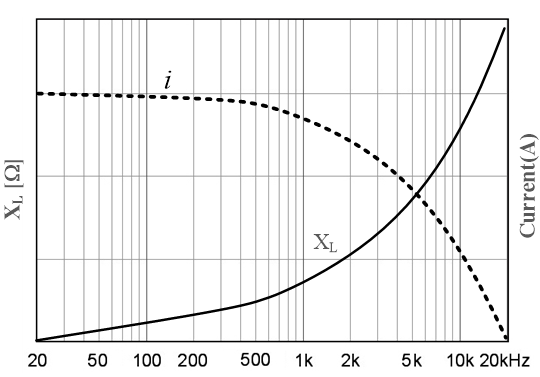
그림 9와 같이 유도성 회로에서 주파수가 낮아지면 리액턴스(X_L)는 작아지고, 주파수가 높아지면 리액턴스가 커진다. 즉, 주파수가 높아지면 저항이 증가하여 전류가 잘 흐르지 않고, 주파수가 낮아지면 저항이 감소하여 전류가 잘 흐르는 특성이 되므로 저역 통과 필터 소자로 사용된다(10장 필터 참조). 그림 9에서 전류 변화는 점선으로 나타낸다.

유도성 리액턴스의 유도

인덕터에 전류(i_L sinωt)가 흐를 때, 유도되는 전압(v_L)은 다음 식으로 구할 수 있다.

v_L (t) = L (di(t))/dt = L d/dt(i_L sinωt) = L∙i_L ωcosωt = ωL∙i_L sin(ωt+90°) = jωL∙i_L sinωt

전류 앞의 j는 전압이 전류보다 90도 앞서는 것을 의미한다.

v_L = jωL∙i_L sinωt
v_L/(i_L sinωt) = jωL = X_L
∴ X_L = jωL = j2πfL[Ω]

*참조; (sinωt)의 미분  →  ωcosωt,  sin(ωt+90°) =  jsinωt

[예제 1]  100mH 코일에 1kHz와 10kHz를 인가한 경우에 각각의 유도성 리액턴스는 얼마인가?
	1kHz를 인가한 경우	XL = 2πfL = 2π⋅1000⋅100⋅10-3 = 628[Ω]
	10kHz를 인가한 경우	XL = 2πfL=2π⋅10000⋅100⋅10-3 = 6280[Ω]
주파수가 높아지면 그림 9와 같이 XL이 커진다.

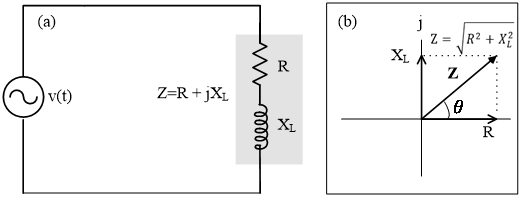
그림 10(a)의 R L 직렬 회로에서 임피던스는 저항과 유도성 리액턴스 값으로부터 구할 수 있다. 인덕터에서 전압 강하는 전류보다 위상이 90도 빠르므로 유도성 리액턴스를 직각 좌표에 나타내면 그림 10(b)와 같이 jX_L이 된다. 따라서 임피던스는 (3) 식과 같이 나타낸다. 크기는 저항 값과 유도성 리액턴스 값의 벡터 합이므로 (4) 식으로 계산한다.

Z = R + jX_L [Ω] (3)

Z = √(R²+X_L² )[Ω],   θ = tan^-1 (X_L/R)°      (4)

[예제 2]  그림 11(a) 회로의 임피던스와 전압과 전류의 위상 차는 얼마인가?

Z = √(R²+X_L² ) = √(4²+3² ) = √25 = 5[Ω]

θ = tan^-1 (3/4) = 36.9°

Z=5∠36.9°

그림 11(c)의 저항 회로에서 합성 저항은 7Ω이 된다.