글 | 강성훈
믹서, 앰프, 마이크 등 음향 기기들의 스펙을 보면 임피던스(impedance)라는 용어가 나온다. 입력 임피던스(input impedance), 출력 임피던스(output impedance), 종단 임피던스(terminating impedance), 정합 임피던스(matched impedance) 등등 많은 용어들이 있다. 임피던스는 믹서, 앰프, 스피커의 특성을 이해하는데 아주 중요하다. 음향 수학 코너에서는 임피던스와 관련된 내용을 다음과 같은 순서대로 설명해 간다.
1. 임피던스란; 저항과 임피던스, 유도성 회로, 용량성 회로, 유도성 용량성 회로,
스피커의 임피던스, 앰프의 출력 임피던스, 스피커 레벨과 라인 레벨 임피던스
2. 기기의 입출력 임피던스 구하기
3.임피던스 매칭
4. 임피던스 브리징
먼저, 전기 저항(electrical resistance, R)을 생각해 본다. 간단하게 건전지와 저항(resistor) 하나만 있는 회로를 생각해 본다. 건전지는 전압을 발생시켜 회로에 전류를 흘리게 되고, 이때 저항은 이 전류를 방해한다. 그러므로 저항의 값이 크면, 전류는 적게 흐르게 된다. 이렇게 전류의 흐름을 방해하면서 저항의 양단에 전압 차가 발생된다. 이러한 현상은 옴의 법칙을 사용해서 계산할 수 있다.
그러나 회로의 전압원이 교류이면 문제가 복잡해진다. 교류 회로에는 전기 저항 이외에도 전류에 영향을 미치는 두 가지 다른 요소가 있기 때문이다. 이것은 코일과 콘덴서이고, 이것들도 저항과 같은 역할을 하지만, 다른 점은 신호 전압이 주파수에 따라서 변하는 전류에 대한 저항이라는 것이다.

음향 기기의 회로는 저항, 커패시터, 인덕터가 조합되어 설계되어 있고,
트랜지스터와 IC와 같은 능동 소자들이 같이 들어 있다. 이때 저항, 커패시터,
인덕터가 포함된 복잡한 회로의 저항을 하나로 생각하고, 이것을
임피던스(impedance)라고 부른다. 임피던스는 Z로 표시하고, 단위는 저항과 같이 옴을 사용한다. 임피던스는 그림 1과 같이 저항과 리액턴스로 구성되어 있는 복소수이다. 그림 1에서 j는 90°회전 연산자로서 허수를 의미한다. 이와 같이 임피던스를 이해하는데는 복소수를 먼저 이해해야 한다.
1. 복소수
1) 실수와 허수
일상에서 사용하는 1, 2, 3, … 은 실수(實數, real number;Re)라고 한다. 양수이든 음수이든 제곱을 하면 전부 양수가 된다.
그런데 제곱을 해서 음수가 나오는 수가 있다. 어떤 수를 2번 곱해서
-1이 되는 수이고, 이것은 실수만으로는 나타낼 수 없으므로 허수(虛數, imaginary number; Im) j를 도입한다. 실수와 허수가 더해진 수를 복소수라고 하고, 그림 2와 같이 복소 평면에 나타낸다.
| 실수 | -10, -5, -1, 0.5, 1, 1/3, 4, 10, 33 |
| 허수 | -j10, -j5, j1, j5, j10, j220 |
| 복소수 | 3+j2, 4+ j10, p+ j 3/2 |
수학적으로 j 값은 ![]() 과 같다. 따라서 +j2에 j를 곱하면 -2가 된다.
과 같다. 따라서 +j2에 j를 곱하면 -2가 된다.
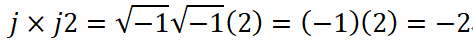
이것은 양의 실수에 j 을 곱하면 음의 실수가 되므로 복소 평면 위에서 180°회전한 것이다.
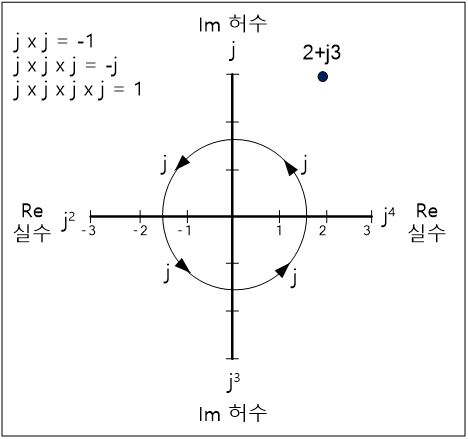
양의 실수 2에 j를 곱하면 +j2가 된다. 즉, +2에 곱한 j는 +2를 90°회전시켜 j축으로 이동하는 것이다. 이와 마찬가지로 +2에 –j를 곱하면 +2는 -90°회전하여 –j축으로 이동한다. 즉, +j는 90°회전시키는 것이고, j (j×j=-1)은 180°회전시키는 것이다(그림 3). 따라서 j를 회전 연산자라고 한다.
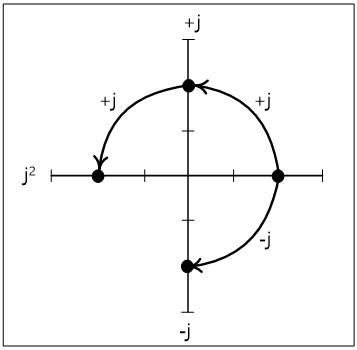
의한 수의 위치 변화
음향 수학
j는 회전 연산자이므로 위상을 90°변화시키는 것과 같다.
- sin(θ-90) = -j sinθ, sin(θ+90) = j sin θ
- 유도성 리액턴스 XL = jωL → 위상이 90°앞섬
- 용량성 리액턴스 XC = -jωC → 위상이 90°늦음
- v(t) = j I sinωt → 전압이 전류보다 위상이 90°앞섬
- i(t) = j V sinωt → 전류가 전압보다 위상이 90°앞섬
2) 복소수의 직각 좌표 형식
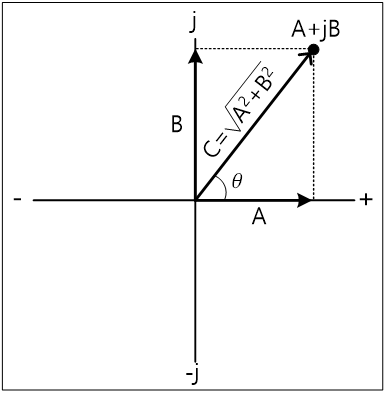
페이저 양을 표시하는데는 직각 좌표 형식과 극 좌표 형식이 있다. 이들을 회로 해석에 사용할 때 어느 형식이 좋은지는 경우에 따라서 다르다. 페이저에는 크기와 위상의 두 값이 함께 포함되어 있다. 페이저 양을 직각 좌표 형식으로 나타내면, 다음과 같이 좌표의 실수(A)와 허수(B)의 합이 된다.
A+jB
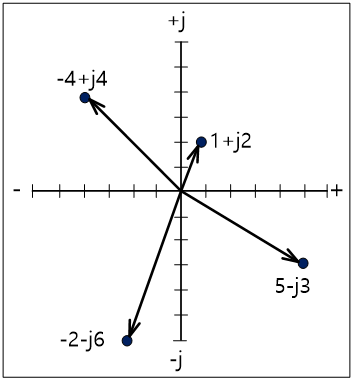
그림 4에는 1+j2, -4+j4, -2-j6, 5-j3의 페이저 양으로 복소 평면에 표시한 것이다. 직각 좌표 형식에서는 페이저를 실수축, 허수축과 직각으로 만나는 점이 실수 값과 허수 값이다. 페이저 양을 복소 평면 위에 그래프로 나타낼 때는 원점에서 그 페이저 점까지 화살표를 그린다. 그림 5는 실수와 허수의 합의 크기를 구하는 그림이다. 실수와 허수가 직각을 이루고 있으므로 피타고라스 정리로 크기를 구한다.
3) 복소수의 극 좌표 형식
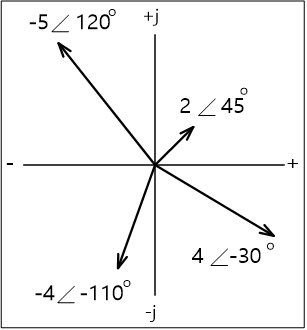
극 좌표 형식(polar form)은 페이저 양을 페이저의 크기(C)와 실수축을 기준으로 한 각도(θ)로 나타낸다.
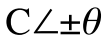
![]() ,
, ![]() ,
, ![]() ,
, ![]() 는 극좌표 형식으로 나타낸 페이저 양이다(그림 6). 여기에서 맨 앞의 숫자는 크기, 기호 다음의 숫자는 각도이다. 어떠한 페이저라도 극 좌표 형식과 직각 좌표 형식으로 모두 나타낼 수 있다.
는 극좌표 형식으로 나타낸 페이저 양이다(그림 6). 여기에서 맨 앞의 숫자는 크기, 기호 다음의 숫자는 각도이다. 어떠한 페이저라도 극 좌표 형식과 직각 좌표 형식으로 모두 나타낼 수 있다.
사인파로 나타낸 전압을 극좌표 형식으로 나타내면 다음과 같이 나타낼 수 있다.
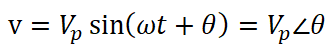
페이저 양













